JENIS BANGUN DATAR & SIFATNYA
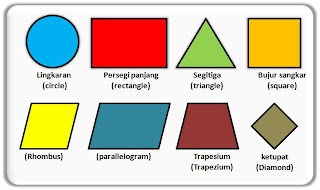 |
| Macam-macam BANGUN DATAR |
Jenis bangun datar bermacam-macam, antara lain persegi, persegi
panjang, segitiga, jajar genjang, trapesium, layang-layang, belah
ketupat, dan lingkaran.
Nama-nama Bangun Datar :
1. Persegi
2. Persegi panjang
3. Segitiga
a. Berdasarkan besar sudut
Nama-nama Bangun Datar :
- Persegi Panjang, yaitu bangun datar yang mempunyai sisi berhadapan yang sama panjang, dan memiliki empat buah titik sudut siku-siku.
- Persegi, yaitu persegi panjang yang semua sisinya sama panjang.
- Segitiga, yaitu bangun datar yang terbentuk oleh tiga buah titik yang tidak segaris.. macam macamnya: segitiga sama sisi, segitiga sama kaki, segitiga siku-siku, segitiga sembarang
- Jajar Genjang, yaitu segi empat yang sisinya sepasang-sepasang sama panjang dan sejajar.
- Trapesium, yaitu segi empat yang memiliki tepat sepasang sisi yang sejajar.
- Layang-layang, yaitu segi empat yang salah satu diagonalnya memotong tegak lurus sumbu diagonal lainnya.
- Belah Ketupat, yaitu segi empat yang semua sisinya sama panjang dan kedua diagonalnya saling berpotongan tegak lurus.
- Lingkaran, yaitu bangun datar yang terbentuk dari himpunan semua titik persekitaran yang mengelilingi suatu titik asal dengan jarak yang sama. jarak tersebut biasanya dinamakan r, atau radius, atau jari-jari.
1. Persegi
- Mempunyai 4 sisi
- Keempat sisinya sama panjang
- Diagonalnya membagi 2 sama panjang
- Keempat sudutnya sama besar
- Mempunyai 4 simetri lipat
- Mempunyai 4 simetri putar
2. Persegi panjang
- Mempunyai 4 sisi
- Sisi-sisi yang berhadapan sejajar dan sama panjang
- Diagonalnya membagi dua sama panjang
- Keempat sudutnya sama besar
- Mempunyai 2 simetri lipat
- Mempunyai 2 simetri putar
- Mempunyai 3 sisi
a. Berdasarkan besar sudut
- Segitiga lancip : segitiga yang besar sudutnya kurang dari 90
- Segitiga siku-siku : segitiga yang besar sudutnya 90
- Segitiga tumpul : segitiga yang besar sudutnya lebih dari 90
- Segitiga sebarang : segitiga yang ketiga sisinya tidak sama panjang
- Segitiga sama sisi : segitiga yang ketiga sisinya sama panjang
- Segitiga sama kaki : segitiga yang dua sisinya sama panjang
4. Jajar genjang
- Mempunyai 4 sisi
- Sisi-sisi yang berhadapan sama panjang dan sejajar
- Diagonalnya saling membagi dua sama panjang
- Sudut-sudut yang berhadapan sama besar
- Tidak mempunyai simetri lipat
- Mempunyai 2 simetri putar
5. Trapesium
- Mempunyai 4 sisi
- Sisi-sisinya tidak sama panjang
- Diagonalnya tidak membagi dua sama panjang
- Mempunyai 1 simetri putar
6. Layang-layang
- Mempunyai 4 sisi
- Mempunyai 2 pasang sisi yang sama panjang
- Diagonalnya saling tegak lurus tetapi tidak semua diagonal membagi dua sama panjang
- Sudut-sudut yang berhadapan tidak semua sama besar
- Mempunyai 1 simetri lipat
- Mempunyai 1 simetri putar
7. Belah ketupat
- Mempunyai 4 sisi
- Keempat sisinya sama panjang
- Sudut-sudut yang berhadapan sama besar
- Diagonalnya saling tegak lurus membagi dua sama panjang
- Mempunyai 2 simetri lipat
- Mempunyai 2 simetri putar
8. Lingkaran
a. 48 cm
b. 24 cm
c. 20 cm
d. 16 cm
Pembahasan :
Keliling = 6 + 8 + 10
= 24 cm
Jawaban : b
3. Keliling bangun di bawah adalah...
a. 43 cm
b. 56 cm
c. 66 cm
d. 72 cm
Pembahasan :
a. 39,25 cm²
b. 117,75 cm²
c. 157 cm²
d. 196,25 cm²
Pembahasan :
Luas I = ½ luas lingkaran besar
= ½ x л x r x r
= ½ x 3,14 x 10 x 10
= 157 cm²
Luas II = ½ luas lingkaran kecil
= ½ x 3,14 x 5 x 5
= 39,25 cm²
Luas bangun dimaksud = Luas I - Luas II
= 157 - 39,25
= 117,75 cm²
Jawaban : b
7. Luas bangun di bawah ini adalah ....
a. 200 cm²
b. 360 cm²
c. 400 cm²
d. 480 cm²
Pembahasan :
Bangun di atas adalah gabungan dua trapesium siku-siku dengan ukuran
atas (a) = 18 cm
bawah (b) = 24=2 cm
tinggi (t) = 10 cm
Luas I = ½ x (a+b) x t
= ½ x (18 + 22) x 10
= ½ x 40 x 10
= 200 cm²
Luas seluruhnya = 2 x 200
= 400 cm²
jawaban : c
8. Luas bangun gabungan di bawah adalah.... cm²
a. 96
b. 157
c. 253
d. 314
Pembahasan :
Bangun di atas adalah gabungan segitiga dan setengah lingkaran
alas segitiga (a) = 16 cm
tinggi segitiga (t) = 12 cm
jari- jari lingkaran = 20 : 2 = 10 cm
Luas I = ½ x a x t
= ½ x 16 x 12
= 96 cm²
Luas II = ½ x л x r x r
= ½ x 3,14 x 10 x 10
= 157 cm²
Luas seluruhnya = Luas I + Luas II
= 96 + 157
= 253 cm²
jawaban : c
9. Luas daerah yang diarsir pada gambar berikut adalah....
a. 86 cm²
b. 96 cm²
c. 314 cm²
d. 400 cm²
Pembahasan :
Luas daerah yang diarsir adalah luas persegi dikurangi luas sebuah lingkaran.
sisi persegi (s) = 20 cm
jari-jari lingkaran (r) = 20 : 2 = 10 cm
Luas I = s x s
= 20 x 20
= 400 cm²
Luas II = л x r x r
10. Luas bangun ABCDEF di bawah adalah....
a. 105 cm²
b. 117 cm²
c. 124 cm²
d. 135 cm²
Pembahasan :
Kita bagi bangun di atas menjadi tiga bagian seperti gambar berikut
Bangun I dan III adalah trapesium
Bangun II adalah persegi
Luas I = ½ x (a+b) x t
= ½ x (7 + 10) x 4
= ½ x 17 x 4 = 34 cm²
Luas II = s x s
= 7 x 7 = 49 cm²
Luas bangun gabungan = Luas I + Luas II + Luas III
= 34 + 49 + 34
= 117 cm²
Jawaban : b
11.Luas bangun di bawah adalah....
a. 84 cm²
b. 108 cm²
c. 216 cm²
d. 384cm²
Pembahasan :Kita bagi bangun di atas menjadi tiga bagian seperti gambar berikut
Bangun I dan II adalah trapesium dengan ukuran a = 6 cm, b = 15 cm dan t = 8 cm
bangun III adalah layang-layang dengan ukuran d₁ = 8 + 8 = 16 cm dan d₂ = 6 + 21 = 27 cm
Luas I = ½ x (6+15) x 8
= ½ x 21 x 8
= 84 cm²
Luas seluruhnya = Luas I + Luas II + Luas III
= 84 + 84 + 216
= 384 cm²
Jawaban : d
12. Tentukan luas bangun berikut !
a. 48 cm²
b. 96 cm²
c. 144 cm²
d. 192 cm²
Pembahasan :
Bangun di atas terdiri dari dua bangun datar. Bangun pertama adalah jajar genjang dengan ukuran alas 12 cm dan tinggi 8 cm, sedangkan bangun kedua adalah belah ketupat dengan ukuran d₁ = 2x8 = 16 cm dan d₂ = 2x6 = 12 cm.
Luas I = a x t
= 12 x 8
= 96 cm²
Luas II = ½ x d₁ x d₂
= ½ x 16 x 12
= 96 cm²
Luas keseluruhan = Luas I + Luas II
= 96 + 96
= 192 cm²
Jawaban : d
13. Tentukan luas bangun berikut !
a.290,75 cm²
b.330 cm²
c.361,4 cm²
d.369,25 cm²
Pembahasan :
Bangun di atas adalah persegi panjang yang dipotong dengan setengah lingkaran. Persegi panjang berukuran p = 22 cm dan lebar = 15 cm. Setengah lingkaran berukuran diameter 22 - (6 +6) = 10 cm, sehingga jari-jari lingkaran = 5 cm.
Luas I = p x l
= 22 x 15
= 330 cm²
Luas II = ½ x π x r x r
= ½ x 3,14 x 5 x 5
= 39,25 cm²
Luas seluruhnya = Luas I - Luas II
= 330 - 39,25
= 290,75 cm²
Jawaban : a
14. Keliling bangun pada nomer 13 adalah.... cm
a.48,3 cm
b.74 cm
c.79,7 cm
d.82,7 cm
Keliling = 15 + 22 + 15 + 6 + keliling ½ lingkaran + 6
= 30 + 34 + (½ x π x d)
= 64 + (½ x 3,14 x 10)
= 64 + 15,7
= 79,7 cm
15. Tentukan Luas daerah yang diarsir berikut !
a. 154 cm²
b. 224 cm²
c. 392 cm²
d. 616 cm²
Pembahasan :
Daerah yang diarsir adalah bangun lingkaran yang dilubangi bangun berbentuk belah ketupat. Jari-jari lingkaran = 28 : 2 = 14 cm, sedangkan belah ketupat mempunyai ukuran d₁ = d₂ = 28 cm.
Luas I = π x r x r
= ²²/₇ x 14 x 14
= 616 cm²
Luas II = ½ x d₁ x d₂
= ½ x 28 x 28
= 392 cm²
Luas daerah yang diarsir = Luas I - Luas II
= 616 - 392
= 224 cm²
Jawaban : b
- Mempunyai simteri lipat yang tak terbatas
- Mempunyai simetri putar yang tak terbatas
Berikut ini kami berikan kumpulan rumus untuk mencari luas dan keliling bangun datar yang lengkap untuk anda,:
Pertanyaan:
a. Tentukan luas persegi panjang EFGH!
b. Tentukan keliling persegi panjang EFGH!
Jawaban:
a. Luas persegi panjang EFGH = p x l
= 10 cm x 5 cm
= 50 cm2.
Jadi, luas persegi panjang EFGH adalah 50 cm2.
b. Keliling persegi panjang EFGH = 2 x (p + l)
= 2 x (10 cm + 5 cm)
= 2 x 15 cm.
= 30 cm Jadi, keliling persegi panjang EFGH adalah 30 cm.
2. Perhatikan persegi ABCD berikut ini!
Pertanyaan
a. Tentukan luas persegi!
b. Tentukan keliling persegi!
Jawaban:
a. Luas persegi ABCD = s x s
= 5 cm x 5 cm
= 25 cm2.
Jadi, luas persegi ABCD adalah 25 cm2.
b. Keliling persegi ABCD = 4 x s
= 4 x 5 cm
= 20 cm.
Jadi, keliling persegi ABCD adalah 20 c
3. Perhatikan segitiga KLM berikut ini!
Pertanyaan:
a. Tentukan luas segitiga KLM!
b. Tentukan keliling segitiga KLM!
Jawaban:
a. Luas segitiga KLM = ½ x a x t
= ½ x 3 cm x 4 cm
= ½ x 12 cm2.
= 6 cm2
Jadi, luas segitiga KLM adalah 6 cm2.
Catatan:
1. Menentukan tinggi dan alas segita adalah dengan cara; tinggi harus tegak lurus dengan alasnya
2. Pada segitiga KLM di atas untuk penentuan tinggi (t) ada dua cara:
– Dengan tinggi AD dan alas BC
– Dengan tinggi AB dan alas AC (pada pembahasan soal ini kita memilik yang kedua)
b. Keliling segitiga KLM = s + s + s
= AC + AB + BC
= 3 cm + 4 cm + 5 cm
= 12 cm.
Jadi, keliling segitiga KLM adalah 12 cm.
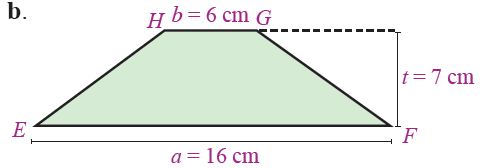
4. Perhatikan trapesium EFGH berikut ini!
Panjang EH = FG = 8 cm.
Pertanyaan:
a. Tentukan luas trapesium EFGH!
b. Tentukan keliling trapesium EFGH!
Jawaban:
a. Luas trapesium EFGH = ½ x (a + b) x t
= ½ x (16 cm + 6 cm) x 7 cm
= ½ x 22 cm x 7 cm
= 11 cm x 7 cm
= 77 cm2
Jadi, luas trapesium EFGH adalah 77 cm2.
b. Keliling trapesium EFGH = s + s + s + s
= EF + FG + GH + HE
= 16 cm + 8 cm + 6 cm + 8 cm
= 38 cm.
Jadi, keliling trapesium EFGH adalah 38 cm.
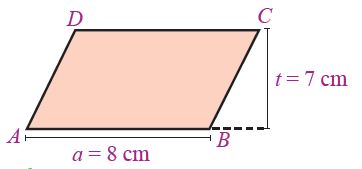
5. Perhatikan jajaran genjang ABCD berikut ini!
Panjang BC = DA = 8 cm. Pertanyaan:
a. Tentukan luas jajaran genjang ABCD!
b. Tentukan keliling jajaran genjang ABCD! Jawaban:
a. Luas jajaran genjang ABCD = a x t
= 8 cm x 7 cm
= 56 cm2
Jadi, luas jajaran genjang ABCD adalah 56 cm2.
b. Keliling jajaran genjang ABCD = s + s + s + s
= AB + BC + CD + DA
= 8 cm + 8 cm + 8 cm + 8 cm
= 32 cm. Jadi, keliling jajaran genjang ABCD adalah 32 cm.
6. Perhatikan belah ketupat berikut ini!
Panjang AC = 12 cm
Panjang BD = 16 cm
Pertanyaan:
a. Tentukan luas belah ketupat ABCD!
b. Tentukan keliling belah ketupat ABCD!
Jawaban:
a. Luas belah ketupat ABCD = ½ x d1 x d2
= ½ x AC x BD
= ½ x 12 cm x 16 cm
= 96 cm2Jadi, luas belah ketupat ABCD adalah 96 cm2.
b. Keliling belah ketupat ABCD = s + s + s + s
= AB + BC + CD + DA
= 4 x s
= 4 x 10 cm
= 40 cm Jadi, keliling belah ketupat ABCD adalah 40 cm.
7. Perhatikan layang layang ABCD berikut ini!
Panjang BC = panjang CD
Panjang AB = panjang AD
Pertanyaan:
a. Tentukan luas layang layang ABCD!
b. Tentukan keliling layang layang ABCD!
Jawaban:
a. Luas layang layang ABCD = ½ x d1 x d2
= ½ x AC x BD
= ½ x 30 cm x 15 cm
= 225 cm2
Jadi, luas layang layang ABCD adalah 225 cm2.
b. Keliling layang layang ABCD = 2 x (x + y)
= 2 x (AB + BC)
= 2 x (12 cm + 22 cm)
= 2 x 34 cm
= 68 cm Jadi, keliling layang layang ABCD adalah 68 cm.
8. Perhatikan lingkaran berikut ini!
Pertanyaan:
a. Tentukan luas lingkaran!
b. Tentukan keliling lingkaran!
Jawaban:
a. Luas lingkaran = πr2
= 22/7 x 7 cm x 7 cm
= 154 cm2
Jadi, luas lingkaran adalah 154 cm2.
b. Keliling lingkaran = πd
= 22/7 x 14 cm
= 44 cm
Jadi, keliling lingkaran adalah 44 cm.
- Persegi
Luas = s x s
Keliling = 4 x s
Ket :
s = sisi
- Persegi Panjang
Luas = p x l
Keliling = 2 x ( p + l )
Ket :
p = panjang
l = lebar - Segitiga
Luas = 1/2 x a x t
Keliling = sisi a + sisi b + sisi c
Ket : a = alas t = tinggi - Jajar Genjang
Luas = a x t
Keliling = 2 x (sisi a + sisi b)
Ket :
a = alas
t = tinggi - Layang – Layang
Luas = 1/2 x d1 x d2
Keliling = 2 x (sisi a + sisi b)
Ket :
d1 = diagonal 1
d2 = diagonal 2 - Belah Ketupat
Luas = 1/2 x d1 x d2
Keliling = 4 x sisi
Ket :
d1 = diagonal 1
d2 = diagonal 2 - Trapesium
Luas = 1/2 x (a + c) x t
Keliling = sisi a +sisi b +sisi c +sisi d
Ket :
a = alas
c = sisi yang sejajar dengan alas - Lingkaran
Luas = π x r x r
Keliling = 2 x π x r = π x d
Ket :
r = jari – jari
d = diameter
CONTOH SOAL
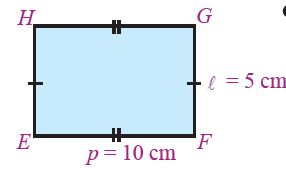 |
a. Tentukan luas persegi panjang EFGH!
b. Tentukan keliling persegi panjang EFGH!
a. Luas persegi panjang EFGH = p x l
= 10 cm x 5 cm
= 50 cm2.
Jadi, luas persegi panjang EFGH adalah 50 cm2.
b. Keliling persegi panjang EFGH = 2 x (p + l)
= 2 x (10 cm + 5 cm)
= 2 x 15 cm.
= 30 cm Jadi, keliling persegi panjang EFGH adalah 30 cm.
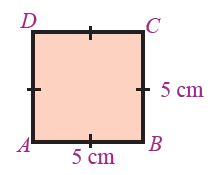 |
a. Tentukan luas persegi!
b. Tentukan keliling persegi!
Jawaban:
a. Luas persegi ABCD = s x s
= 5 cm x 5 cm
= 25 cm2.
Jadi, luas persegi ABCD adalah 25 cm2.
b. Keliling persegi ABCD = 4 x s
= 4 x 5 cm
= 20 cm.
Jadi, keliling persegi ABCD adalah 20 c
3. Perhatikan segitiga KLM berikut ini!
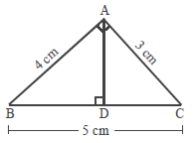 |
a. Tentukan luas segitiga KLM!
b. Tentukan keliling segitiga KLM!
a. Luas segitiga KLM = ½ x a x t
= ½ x 3 cm x 4 cm
= ½ x 12 cm2.
= 6 cm2
Jadi, luas segitiga KLM adalah 6 cm2.
Catatan:
1. Menentukan tinggi dan alas segita adalah dengan cara; tinggi harus tegak lurus dengan alasnya
2. Pada segitiga KLM di atas untuk penentuan tinggi (t) ada dua cara:
– Dengan tinggi AD dan alas BC
– Dengan tinggi AB dan alas AC (pada pembahasan soal ini kita memilik yang kedua)
b. Keliling segitiga KLM = s + s + s
= AC + AB + BC
= 3 cm + 4 cm + 5 cm
= 12 cm.
Jadi, keliling segitiga KLM adalah 12 cm.
4. Perhatikan trapesium EFGH berikut ini!
 |
Pertanyaan:
a. Tentukan luas trapesium EFGH!
b. Tentukan keliling trapesium EFGH!
a. Luas trapesium EFGH = ½ x (a + b) x t
= ½ x (16 cm + 6 cm) x 7 cm
= ½ x 22 cm x 7 cm
= 11 cm x 7 cm
= 77 cm2
Jadi, luas trapesium EFGH adalah 77 cm2.
b. Keliling trapesium EFGH = s + s + s + s
= EF + FG + GH + HE
= 16 cm + 8 cm + 6 cm + 8 cm
= 38 cm.
Jadi, keliling trapesium EFGH adalah 38 cm.
5. Perhatikan jajaran genjang ABCD berikut ini!
 |
a. Tentukan luas jajaran genjang ABCD!
b. Tentukan keliling jajaran genjang ABCD! Jawaban:
a. Luas jajaran genjang ABCD = a x t
= 8 cm x 7 cm
= 56 cm2
Jadi, luas jajaran genjang ABCD adalah 56 cm2.
b. Keliling jajaran genjang ABCD = s + s + s + s
= AB + BC + CD + DA
= 8 cm + 8 cm + 8 cm + 8 cm
= 32 cm. Jadi, keliling jajaran genjang ABCD adalah 32 cm.
6. Perhatikan belah ketupat berikut ini!
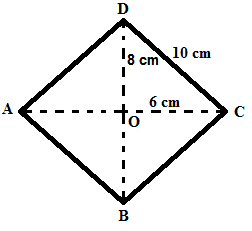 |
Panjang BD = 16 cm
Pertanyaan:
a. Tentukan luas belah ketupat ABCD!
b. Tentukan keliling belah ketupat ABCD!
a. Luas belah ketupat ABCD = ½ x d1 x d2
= ½ x AC x BD
= ½ x 12 cm x 16 cm
= 96 cm2Jadi, luas belah ketupat ABCD adalah 96 cm2.
b. Keliling belah ketupat ABCD = s + s + s + s
= AB + BC + CD + DA
= 4 x s
= 4 x 10 cm
= 40 cm Jadi, keliling belah ketupat ABCD adalah 40 cm.
7. Perhatikan layang layang ABCD berikut ini!
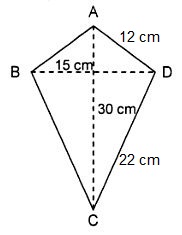 |
Panjang AB = panjang AD
Pertanyaan:
a. Tentukan luas layang layang ABCD!
b. Tentukan keliling layang layang ABCD!
Jawaban:
a. Luas layang layang ABCD = ½ x d1 x d2
= ½ x AC x BD
= ½ x 30 cm x 15 cm
= 225 cm2
Jadi, luas layang layang ABCD adalah 225 cm2.
b. Keliling layang layang ABCD = 2 x (x + y)
= 2 x (AB + BC)
= 2 x (12 cm + 22 cm)
= 2 x 34 cm
= 68 cm Jadi, keliling layang layang ABCD adalah 68 cm.
8. Perhatikan lingkaran berikut ini!
 |
a. Tentukan luas lingkaran!
b. Tentukan keliling lingkaran!
Jawaban:
a. Luas lingkaran = πr2
= 22/7 x 7 cm x 7 cm
= 154 cm2
Jadi, luas lingkaran adalah 154 cm2.
b. Keliling lingkaran = πd
= 22/7 x 14 cm
= 44 cm
Jadi, keliling lingkaran adalah 44 cm.
Bangun datar adalah
bangun dua dimensi yang dibatasi garis-garis lurus atau garis lengkung.
Bangun datar memiliki keliling dan luas. Bangun datar yang dibahas
untuk materi sekolah dasar diantaranya adalah segitiga, persegi, persegi
panjang, jajar genjang, trapesium, belah ketupat, layang-layang dan
lingkaran. Bangun datar-bangun datar tersebut dapat dibentuk menjadi
gabungan bangun datar.
Berikut adalah contoh soal dan pembahasan tentang bangun datar gabungan.
1. Rumus luas trapesium adalah....
a. ½ x alas x tinggi
b. alas x tinggi
c. ½ x (jumlah sisi sejajar) x tinggi
d. ½ x diagonal₁ x diagonal₂
Pembahasan :
a = luas segitiga
b = luas jajar genjang
c = luas trapesium
d = luas layang- layang atau belah ketupat
Jawaban : c
2. Keliling segitiga berikut adalah....
Berikut adalah contoh soal dan pembahasan tentang bangun datar gabungan.
1. Rumus luas trapesium adalah....
a. ½ x alas x tinggi
b. alas x tinggi
c. ½ x (jumlah sisi sejajar) x tinggi
d. ½ x diagonal₁ x diagonal₂
Pembahasan :
a = luas segitiga
b = luas jajar genjang
c = luas trapesium
d = luas layang- layang atau belah ketupat
Jawaban : c
2. Keliling segitiga berikut adalah....
 |
| soal bangun datar gabungan no.2 |
a. 48 cm
b. 24 cm
c. 20 cm
d. 16 cm
Pembahasan :
Keliling = 6 + 8 + 10
= 24 cm
Jawaban : b
3. Keliling bangun di bawah adalah...
 |
| soal bangun datar gabungan no.3 |
a. 43 cm
b. 56 cm
c. 66 cm
d. 72 cm
Pembahasan :
 |
| Pembahasan |
Keliling adalah jumlah garis-garis yang membatasi suatu bangun. Keliling bangun di samping adalah =
18 + 15 + 5 + 10 + 13 + 5 = 66 cm
Jawaban : c
4. Sebuah persegi mempunyai luas 441 cm². Berapa keliling persegi tersebut?
a. 220 cm
b. 129 cm
c. 84 cm
d. 42 cm
Pembahasan :
Luas persegi = s x s
maka s = √441
= 21 cm
keliling persegi = 4 x s
= 4 x 21
= 84 cm
Jawaban : c
5. Keliling bangun di bawah ini adalah...
18 + 15 + 5 + 10 + 13 + 5 = 66 cm
Jawaban : c
4. Sebuah persegi mempunyai luas 441 cm². Berapa keliling persegi tersebut?
a. 220 cm
b. 129 cm
c. 84 cm
d. 42 cm
Pembahasan :
Luas persegi = s x s
maka s = √441
= 21 cm
keliling persegi = 4 x s
= 4 x 21
= 84 cm
Jawaban : c
5. Keliling bangun di bawah ini adalah...
 |
| soal bangun datar gabungan no.5 |
a. 22 cm
b. 33 cm
c. 44 cm
d. 54 cm
Pembahasan :
b. 33 cm
c. 44 cm
d. 54 cm
Pembahasan :
Garis yang membatasi adalah garis lengkung setengah keliling lingkaran dan garis datar diameter.
Maka keliling bangun tersebut
= (½ x л x d) + d
= (½ x ²²/₇ x 21) + 21
= 33 + 21 = 54 cm
Jawaban : d
6. Luas bangun di bawah adalah.....
 |
| soal bangun datar gabungan no.6 |
a. 39,25 cm²
b. 117,75 cm²
c. 157 cm²
d. 196,25 cm²
Pembahasan :
Luas I = ½ luas lingkaran besar
= ½ x л x r x r
= ½ x 3,14 x 10 x 10
= 157 cm²
Luas II = ½ luas lingkaran kecil
= ½ x 3,14 x 5 x 5
= 39,25 cm²
Luas bangun dimaksud = Luas I - Luas II
= 157 - 39,25
= 117,75 cm²
Jawaban : b
7. Luas bangun di bawah ini adalah ....
 |
| soal bangun datar gabungan no.7 |
a. 200 cm²
b. 360 cm²
c. 400 cm²
d. 480 cm²
Pembahasan :
Bangun di atas adalah gabungan dua trapesium siku-siku dengan ukuran
atas (a) = 18 cm
bawah (b) = 24=2 cm
tinggi (t) = 10 cm
Luas I = ½ x (a+b) x t
= ½ x (18 + 22) x 10
= ½ x 40 x 10
= 200 cm²
Luas seluruhnya = 2 x 200
= 400 cm²
jawaban : c
8. Luas bangun gabungan di bawah adalah.... cm²
 |
| soal bangun datar gabungan no.8 |
a. 96
b. 157
c. 253
d. 314
Pembahasan :
Bangun di atas adalah gabungan segitiga dan setengah lingkaran
alas segitiga (a) = 16 cm
tinggi segitiga (t) = 12 cm
jari- jari lingkaran = 20 : 2 = 10 cm
Luas I = ½ x a x t
= ½ x 16 x 12
= 96 cm²
Luas II = ½ x л x r x r
= ½ x 3,14 x 10 x 10
= 157 cm²
Luas seluruhnya = Luas I + Luas II
= 96 + 157
= 253 cm²
jawaban : c
9. Luas daerah yang diarsir pada gambar berikut adalah....
 |
| soal bangun datar gabungan no.9 |
a. 86 cm²
b. 96 cm²
c. 314 cm²
d. 400 cm²
Pembahasan :
Luas daerah yang diarsir adalah luas persegi dikurangi luas sebuah lingkaran.
sisi persegi (s) = 20 cm
jari-jari lingkaran (r) = 20 : 2 = 10 cm
Luas I = s x s
= 20 x 20
= 400 cm²
Luas II = л x r x r
= 3,14 x 10 x 10
= 314 cm²
Luas daerah yang diarsir = Luas I - Luas II
= 400 - 314
= 400 - 314
= 86 cm²
Jawaban : a
10. Luas bangun ABCDEF di bawah adalah....
 |
| soal bangun datar gabungan no.10 |
a. 105 cm²
b. 117 cm²
c. 124 cm²
d. 135 cm²
Pembahasan :
Kita bagi bangun di atas menjadi tiga bagian seperti gambar berikut
 |
| Pembahasan |
Bangun I dan III adalah trapesium
Bangun II adalah persegi
Luas I = ½ x (a+b) x t
= ½ x (7 + 10) x 4
= ½ x 17 x 4 = 34 cm²
Luas II = s x s
= 7 x 7 = 49 cm²
Luas III = ½ x (a+b) x t
= ½ x (7 + 10) x 4
= ½ x 17 x 4 = 34 cm²
Luas bangun gabungan = Luas I + Luas II + Luas III
= 34 + 49 + 34
= 117 cm²
Jawaban : b
11.Luas bangun di bawah adalah....
 |
| soal bangun datar gabungan no11 |
a. 84 cm²
b. 108 cm²
c. 216 cm²
d. 384cm²
Pembahasan :Kita bagi bangun di atas menjadi tiga bagian seperti gambar berikut
 |
| pembahasan |
Bangun I dan II adalah trapesium dengan ukuran a = 6 cm, b = 15 cm dan t = 8 cm
bangun III adalah layang-layang dengan ukuran d₁ = 8 + 8 = 16 cm dan d₂ = 6 + 21 = 27 cm
Luas I = ½ x (6+15) x 8
= ½ x 21 x 8
= 84 cm²
Luas II = ½ x (6+15) x 8
= ½ x 21 x 8
= 84 cm²
Luas III = ½ x d₁ x d₂
= ½ x 16 x 27
= 216 cm²
Luas seluruhnya = Luas I + Luas II + Luas III
= 84 + 84 + 216
= 384 cm²
Jawaban : d
12. Tentukan luas bangun berikut !
 |
| soal bangun datar gabungan no.12 |
a. 48 cm²
b. 96 cm²
c. 144 cm²
d. 192 cm²
Pembahasan :
Bangun di atas terdiri dari dua bangun datar. Bangun pertama adalah jajar genjang dengan ukuran alas 12 cm dan tinggi 8 cm, sedangkan bangun kedua adalah belah ketupat dengan ukuran d₁ = 2x8 = 16 cm dan d₂ = 2x6 = 12 cm.
Luas I = a x t
= 12 x 8
= 96 cm²
Luas II = ½ x d₁ x d₂
= ½ x 16 x 12
= 96 cm²
Luas keseluruhan = Luas I + Luas II
= 96 + 96
= 192 cm²
Jawaban : d
13. Tentukan luas bangun berikut !
 |
| soal bangun datar gabungan no.13 |
a.290,75 cm²
b.330 cm²
c.361,4 cm²
d.369,25 cm²
Pembahasan :
Bangun di atas adalah persegi panjang yang dipotong dengan setengah lingkaran. Persegi panjang berukuran p = 22 cm dan lebar = 15 cm. Setengah lingkaran berukuran diameter 22 - (6 +6) = 10 cm, sehingga jari-jari lingkaran = 5 cm.
Luas I = p x l
= 22 x 15
= 330 cm²
Luas II = ½ x π x r x r
= ½ x 3,14 x 5 x 5
= 39,25 cm²
Luas seluruhnya = Luas I - Luas II
= 330 - 39,25
= 290,75 cm²
Jawaban : a
14. Keliling bangun pada nomer 13 adalah.... cm
a.48,3 cm
b.74 cm
c.79,7 cm
d.82,7 cm
Keliling = 15 + 22 + 15 + 6 + keliling ½ lingkaran + 6
= 30 + 34 + (½ x π x d)
= 64 + (½ x 3,14 x 10)
= 64 + 15,7
= 79,7 cm
15. Tentukan Luas daerah yang diarsir berikut !
 |
| soal bangun datar gabungan no.15 |
a. 154 cm²
b. 224 cm²
c. 392 cm²
d. 616 cm²
Pembahasan :
Daerah yang diarsir adalah bangun lingkaran yang dilubangi bangun berbentuk belah ketupat. Jari-jari lingkaran = 28 : 2 = 14 cm, sedangkan belah ketupat mempunyai ukuran d₁ = d₂ = 28 cm.
Luas I = π x r x r
= ²²/₇ x 14 x 14
= 616 cm²
Luas II = ½ x d₁ x d₂
= ½ x 28 x 28
= 392 cm²
Luas daerah yang diarsir = Luas I - Luas II
= 616 - 392
= 224 cm²
Jawaban : b





















0 Comments:
Posting Komentar